لعوناردو داوینچی (Leonardo Fibonacci) در سال ۱۱۷۵م متولد شد و نخستین ریاضیدان بزرگ اروپا در قرن سیزدهم میلادی است. وی به‌دلیل مطرح کردن موضوع «ترتیب اعداد» مورد توجه قرار گرفت. یکی از کارهای او معرفی سری معروف فیبوناچی است که پس از مراجعت از سفرش به مصر در کتابی به نام کتاب حساب آن را معرفی کرد. نسبت‌های معروف فیبوناچی در طبیعت و در اعضای بدن انسان و… نمایانگر اعتبار سری اعداد فیبوناچی و نسبت‌های آن است. ترتیب اعدادی که فیبوناچی سال‌ها قبل بر آن‌ها تأکید کرد، در بازار های مالی و بورس کاربرد فراوانی برای تحلیلگران دارد.
عجایب اعداد فیبوناچی
«عدد فی یا عدد طلایی» از دنباله فیبوناچی مشتق شده است، تصاعد مشهوری که شهرتش تنها به این دلیل نیست که هر جمله با مجموع دو جمله پیشین خود برابری می‌کند، بلکه به این دلیل است که خارج قسمت هر دو جمله به جمله ماقبلش عدد طلایی ۱.۶۱۸ است که به «نسبت طلایی» یا «عدد فی» مشهور است.
لازم است بدانید اولین اعداد این سری عبارت‌اند از:
۱،۱،۲،۳،۵،۸،۱۳،۲۱،۳۴،۵۵،۸۹،۱۴۴،۲۳۳
چرا این دنباله اعداد مشهور شده است؟
سری فیبوناچی رشته‌ای از اعداد است که در آن اعداد غیر از دو عدد اول با محاسبه مجموع دو عدد قبلی ایجاد می‌شوند با وجود گستردگی طبیعت و وجود انواع موجودات پیرامون انسان‌ها، نظم خاصی بر همه‌چیز حاکم است که با پیشرفت علوم بشری، این نظم بیش‌ازپیش مشخص‌تر می‌شود. شاید در زمان یادگیری مفاهیم علمی، بسیاری از موارد بی‌معنی به نظر برسد، اما نظم خاصی در پشت همه‌چیز نهفته است.
ریاضیات یکی از علوم پایه است که کشف اسرار آن، کلید حل معمای موجود در طبیعت است.
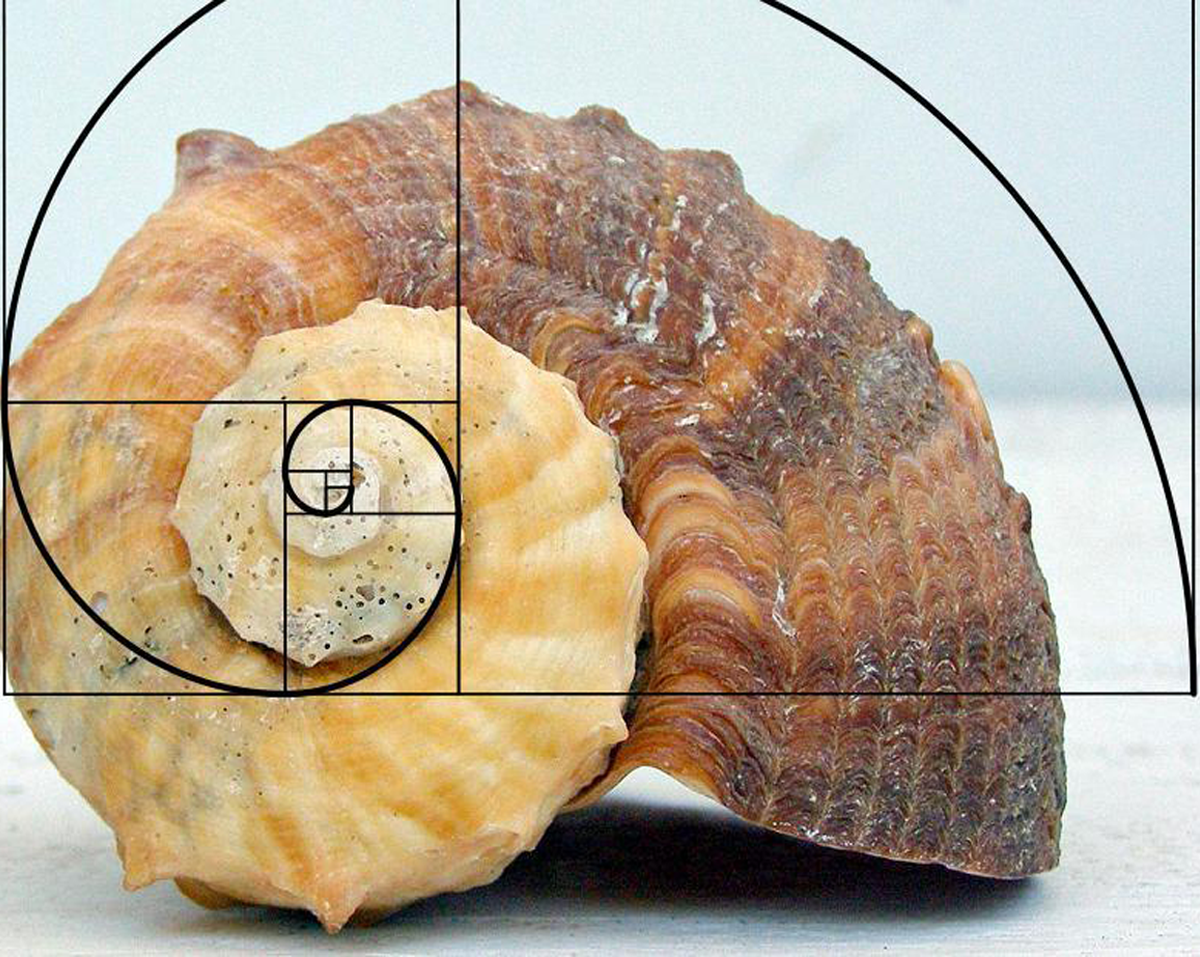
همان‌طور که اشاره شد این اعداد در هستی کشف شده‌اند. در قسمت لاک حلزون از زاویه «فی» استفاده شده است. شاخ و برگ درخت‌ها به‌صورت تصادفی در جهات مختلف رشد نمی‌کنند. اندازه‌گیری زاویه شاخه‌ها نشان می‌دهد که در الگوی رشد آن‌ها، نظمی شبیه دنباله فیبوناچی و نسبت طلایی وجود دارد. درختان با پیروی از این نوع الگوی رشد، قادر هستند درصد بیشتری از نور خورشید را جذب کنند.
دانه‌های آفتابگردان به شکل مارپیچ‌هایی روبروی هم رشد می‌کنند. طبق تحقیقات انجام شده نسبت قطر هر مارپیچ به مارپیچ بعدی ۱.۶۱۸ است. برای درک بهتر مفهوم این اعداد به مثال‌ها و تصاویری که در ادامه می‌آید توجه کنید.
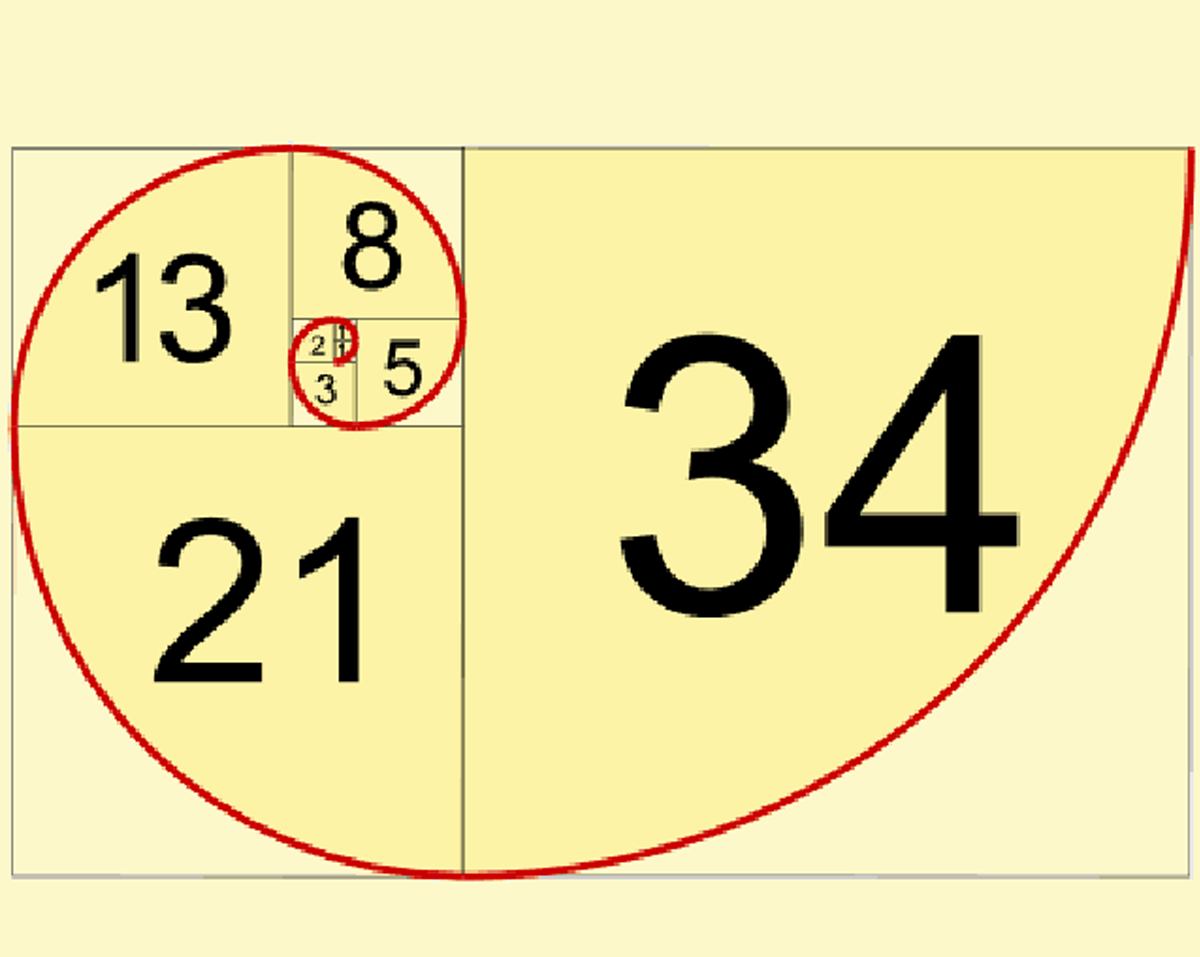
تشکیل مارپیچ با اعداد دنباله‌ی فیبوناچی
همان‌طور که در تصاویر زیر می‌بینید اگر با اعداد دنباله فیبوناچی مربع‌هایی بسازیم، ملاحظه می‌کنید که مربع‌ها چگونه به‌طور منظم و مرتب کنار هم جای می‌گیرند؛ مثلا مربع‌های یک و یک مربع دو را می‌سازند؛ مربع‌های پنج و هشت مربع ۱۳ را ایجاد می‌کنند؛ مربع‌های هشت و ۱۳ مربع ۲۱ را می‌سازند و به همین منوال ادامه می‌یابد. سپس اگر به‌اندازه‌ی طول ضلع مربع‌ها کمان‌هایی رسم شود، در نهایت یک مارپیچ بدست می‌آید که به‌سرعت رشد می‌کند.
معمای زادوولد خرگوش فیبوناچی
برای درک بهتر مفهوم اعداد فیبوناچی به این مثال توجه کنید. فیبوناچی قصد داشت بررسی کند که اگر یک جفت خرگوش نر و ماده داشته باشید، میزان زادوولد آن‌ها چطور خواهد بود.
تصور کنید خرگوش‌ها همین حالا به دنیا آمده‌اند و پس از یک ماه بالغ می‌شوند، دوران بارداری خرگوش ماده یک ماه است و هنگامی‌که به این سن برسد باردار می‌شود. پس‌ازآن یک خرگوش ماده و یک نر به دنیا می‌آیند و البته فرض می‌شود که خرگوش‌ها هرگز نمی‌میرند. به‌این‌ترتیب پس از یک سال چه تعداد خرگوش ماده و چه تعداد نر خواهیم داشت؟
او Fn را برابر با تعداد جفت‌های زاد و ولد شده در ماه nاُم در نظر گرفت. در نتیجه در ماه اول یک جفت، در ماه دوم یک جفت جدید و در ماه سوم هر یک از دو جفت اول یک جفت جدید زاد و ولد می‌کنند، به همین ترتیب هر جفت خود می‌تواند پس از یک ماه جفت دیگری را به دنیا آورد و الگوی تعداد جفت‌های جدید مطابق سری اعداد فیبوناچی است.
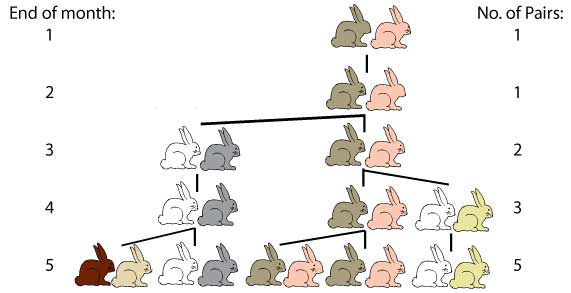سری فیبوناچی برای الگوی تولید مثل خرگوش به صورت زیر است:
۱،۱،۲،۳،۵،۸،۱۳،۲۱،۳۴،۵۵،۸۹،۱۴۴،۲۳۳
سری فیبوناچی چیست؟
سری فیبوناچی رشته‌ای از اعداد است که در آن اعداد غیر از دو عدد اول با محاسبه مجموع دو عدد قبلی ایجاد می‌شوند. در تصویر زیر مشاهده می‌کنید که هر عدد در این تصاعد، حاصل جمع دو عدد قبلی با یکدیگر است.
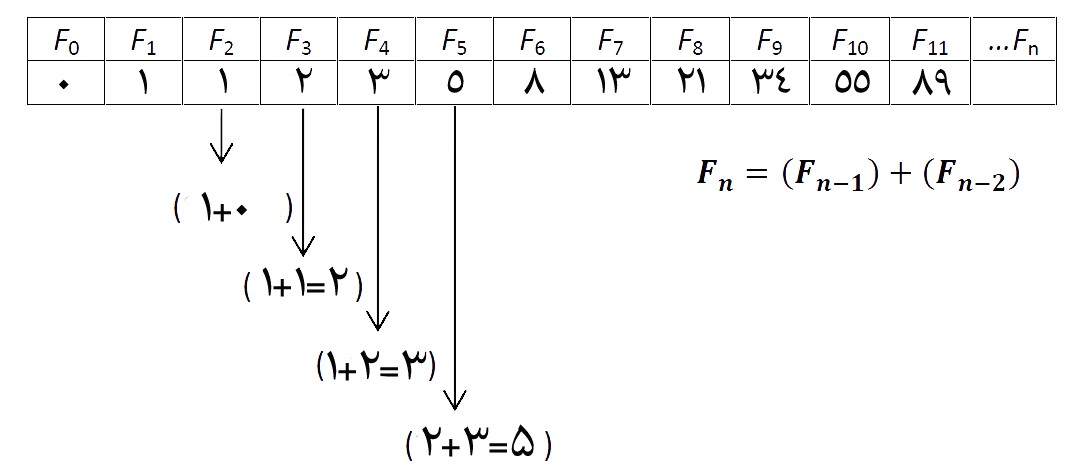همان‌طور که اشاره شد «عدد فی» از دنباله فیبوناچی مشتق شده است، سری مشهوری که شهرتش تنها به این دلیل نیست که هر جمله با مجموع دو جمله‌ی پیشین خود برابری می‌کند، بلکه به این دلیل است که خارج‌قسمت هر دو جمله‌ی کنار هم خاصیت حیرت‌انگیزی نزدیک به عدد ۱.۶۱۸ را دارد که به «نسبت طلایی» مشهور است. به‌عنوان‌مثال تقسیم ۸۹ بر ۵۵ یا ۱۴۴ بر ۸۹ یا ۲۳۳ بر ۱۴۴ همگی برابر با ۱.۶۱۸ می‌شود.
کاربرد فیبوناچی در تحلیل تکنیکال سهام
حال که با مفهوم سری اعداد فیبوناچی آشنا شدید، لازم است با کاربرد آن درتحلیل تکنیکال بازار سهام آشنا شوید. امروزه برای معامله‌گران این موضوع اهمیت دارد که بفهمند چگونه این اعداد وارد بازی سهام می‌شوند و نقش خود را در بازار بر عهده می‌گیرند.
در ابتدای ایجاد یک بازار، منطقی است که بگوییم کاری که در بازارها انجام می‌شود، بسیار ساده است. افراد با خریدوفروش‌های خود یک بازار را به وجود می‌آورند؛ اما به‌تدریج پیچیدگی بازارها افزایش می‌یابد. در حال حاضر بسیاری از خبرگان بازار سهام چیزی را نمی‌خرند، به دلیل اینکه «احساس می‌کنند آن را دوست دارند یا ندارند». اکنون تحلیلگران تکنیکال سعی می‌کنند سریع و دقیق‌تر به این نکته پی‌ببرند که در چه نقطه‌ای از نمودار باید وارد و در چه نقطه‌ای از آن خارج شد.
درصورتی‌که به پیچیدگی بازار اعتقاد داشته باشیم، منطقی است که بیشتر معامله‌گران در آینده‌ای نزدیک به‌طرف روش‌های علمی‌تر برای معاملات خود سوق پیدا کنند. قبول اهمیت نقاط فیبوناچی توسط معامله‌گران درنهایت به‌جایی ختم می‌شود که هرگاه نمودار به سمت این نقاط حرکت می‌کند، معامله‌گران بتوانند رفتار آن را پیش‌گویی کنند.
با این تفاسیر می‌توان گفت که انواع ابزارهای فیبوناچی در بازارهای مالی، روشی برای تحلیل بازگشت یا ادامه روند هستند. از منظری انواع ابزارهای فیبوناچی نقاط حمایت و مقاومت هستند که با ابزارها و روش‌های گوناگون رسم می‌شوند.
این سطوح بازگشت برخلاف حمایت و مقاومت‌های قبلی که تنها قیمتی خاص را نقطه حساس تلقی می‌کردند می‌توانند قیمتی خاص، خطی مورب یا زمان خاصی را نقطه حساس حمایت یا مقاومت تعریف کنند. در استفاده از ابزارهای فیبوناچی درصدها اهمیتی فوق‌العاده دارند.
عموم این درصدها از نسبت درصدهای بین اعداد فیبوناچی به دست می‌آیند. به‌غیراز چند عدد ابتدای سری اعداد فیبوناچی، هرکدام از اعداد دنباله، تقریبا ۱٫۶۱۸ برابر عدد قبل از خود هستند(نسبت طلایی) و هر عدد ۰٫۶۱۸ برابر عدد بعد از خود است.
این نسبت‌ها به درصد به ترتیب ۱۶۱٫۸ درصد و ۶۱٫۸ درصد می‌شوند. درصدهای دیگری نیز مهم هستند که در ادامه می‌آید. تقسیم عدد اول به عدد دوم سری اعداد فیبوناچی یک‌به‌یک یا به عبارتی ۱۰۰ درصد را نشان می‌دهد.
تقسیم عدد دوم به عدد سوم سری اعداد فیبوناچی ۰٫۵ یا به‌عبارتی ۵۰ درصد را نشان می‌دهد.
در اعداد بالاتر سری اعداد فیبوناچی و تقسیم هر عدد به دو عدد بعد از آن، مشاهده می‌شود حاصل تقسیم به ۳۸٫۲ درصد تمایل می‌کند. در اعداد بالاتر سری اعداد فیبوناچی و تقسیم هر عدد به سه عدد بعد از آن، مشاهده می‌شود حاصل تقسیم به ۲۳٫۶ درصد تمایل دارد.
بدون دیدگاه